測圓海鏡有個數學題, 到現在還是算不出來. 眾邦友們有解法嗎?
測圓海鏡問到
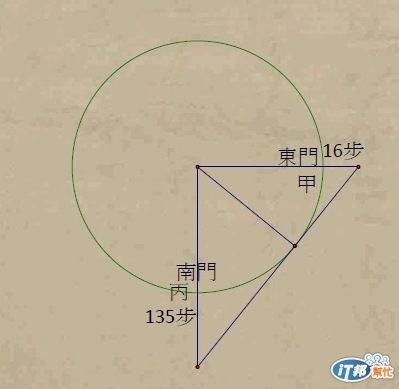
假令有圓城一所, 不知周徑. 丙出南門直行一百三十五步而立, 甲出東門直行一十六步見之. 問徑幾何?
用白話文來講
觀光局要把山寨版的圓樓寫進觀光資料裡面, 縣府提供的資料裡面沒有圓樓的大小和直徑. 於是派了小雨和丁大丙出差到圓樓測量, 到了時候才發現只帶了魯班尺出來. 沒有辦法實際去量圓樓的直徑, 但是發現這個圓樓東南西北各開了一個門, 於是想出用古法來計算.
假設一步六十公分,丁大丙從南門向正南方走了135步停下來. 小雨從東門往正東走16步就看到丁大丙了, 請問這個圓樓的直徑多少?

原理:
已知兩個人走出的範圍唯一直角三角形
直角三角形已知兩邊長,可以用畢氏定理求第三邊長:a^2 + b^2 = c^2
再利用三角形面積的計算方式就可以算出半徑
畢氏定理,與中國商代數學家 商高所提的:『勾三股四弦五』相同
可是 16, 135 都是從城門開始算的
邊長似乎應該是 16+r 和 135+r 才是
![]()
![]()
所以運算式要改為
(16+x) * (135+x) / 2 = Math.Sqrt((16+x)^2 + (135+x) ^ 2) * x / 2
以 wiselou 大大的公式計算
求得直徑為 120*2 = 240
![]()
iT邦幫忙MVPwiselou提到:
Math.Sqrt
外獅佬請用筆算![]()
tecksin提到:
請用筆算
我是用筆....電算的啊![]()
慘
看了運算式求 X
還是解不出來
![]()
antijava提到:
求得直徑為 120*2 = 240
李治的圓城很喜歡用240這個數值![]()
以 wiselou 大大的公式計算
求得直徑為 120*2 = 240
裡面是變數...你怎麼用Math.Sqrt算得出來??????
著令丁大丙疾步至西門
徐步由西門進,直行至東門出
將步數回報予於東門等侯之小雨即可
由西門至東門之步數即為直徑
為什麼是丁大丙去走而不是小雨?
因為丁大丙比較菜
![]()
![]()
![]()
大家似乎都忽略了丁大丙是短腿的"大塊呆",小雨是機器動力POWER非常充足,兩者步伐是不對等的...呵。
剛看完李治的解法...
只有一種感覺....想死![]()
知道用筆算的痛苦了吧![]()
不是...是那個解法用文言文寫,比題目更讓人想死![]()
看看這題的文言文解法
法曰
以丙行步一百三十五步, 再自之得二百四十六萬零三百七十五於上(135^3=2460375).
又以甲行步一十六乘丙行冪一萬八千二百二十五得二十九萬一千六百 (16 * 135 ^2 = 16 * 18225 = 291600)
以乘上位得七千一百七十四億四千五百三十五萬為三乘方 (291600 * 2460375 = 717445350000)
以下省略數百字
如法得二百四十步即城徑也![]()
iT邦幫忙MVPwiselou提到:
想死
所以中國古代的數學家,都是想死又死不掉的嗎??....![]()
[ quote="tecksin" ]以丙行步一百三十五步, 再自之得二百四十六萬零三百七十五於上[ /quote ]
文言文寫完一行算式,用阿拉伯數字已經算完了吧..
![]()